- Published on
Rust入门笔记(六)
- Authors

- Name
- Et cetera
Vectors(Embeddings) 简介
向量用于在数据库中存储文档、图像、视频等复杂的非结构化数据,并查找基于该类型下的相似单位等情况
向量不一定是三维的(可能是更多纬度),之间的距离也不一定必须是 euclidean distance(欧式距离),重要的是它们之间的距离对应于它们的相似性
我们如何找到与给定起始视频最相似的视频? 简单来说,先遍历所有视频,计算它们之间的距离并选择距离最小的视频 - 也称为查找查询视频的 最近邻居;但是这样 O(N)的线性查找成本 💰 太过昂贵
在实际情况下,我们不需要找到最近的视频——找到足够接近的视频也可以.这就是近似最近邻搜索算法(矢量搜索)的用武之地; 目标是次线性地(理想情况下在对数时间内)找到空间中任何点的足够近的最近邻
如何实现查找最近邻居
所有矢量搜索算法背后的基本思想都是相同的 —— 进行一些预处理以识别彼此足够接近的点(有点类似于建立索引);在查询时,使用这个索引来排除大范围的点.并在不排除的少量点内进行线性扫描
几种最先进的矢量搜索算法,例如 HNSW(一种连接近距离顶点并通过固定入口点保持长距离边的图).存在开源项目,例如 Facebook 的 FAISS,以及一些用于高可用性矢量数据库的 PaaS 产品,例如 Pinecone 和 Weaviate
个人实现向量搜索的实现思路
- 在给定的
N个点上构建一个简化的向量搜索索引:
- 随机取 2 个任意可用向量 A 和 B
- 计算这两个向量之间的中点,称为 C
- 构建一个通过 C 并垂直于连接 A 和 B 的线段的
超平面(类似于更高维度的“线”) - 将所有向量分类为超平面
上方或下方,将可用向量分成 2 组 - 对于两个组中的每一个: 如果组的大小大于可配置参数
最大节点大小,则递归地对该组调用此过程以构建子树.否则,使用所有向量(或它们的唯一 ID)构建一个叶节点
因此,我们使用这个随机过程来构建一棵树,其中每个内部节点都是一个超平面定义,左子树是超平面下方的所有向量,右子树是超平面上方的所有向量.向量集不断递归拆分,直到叶节点包含的向量不超过最大节点大小.考虑下图中的例子有五点:
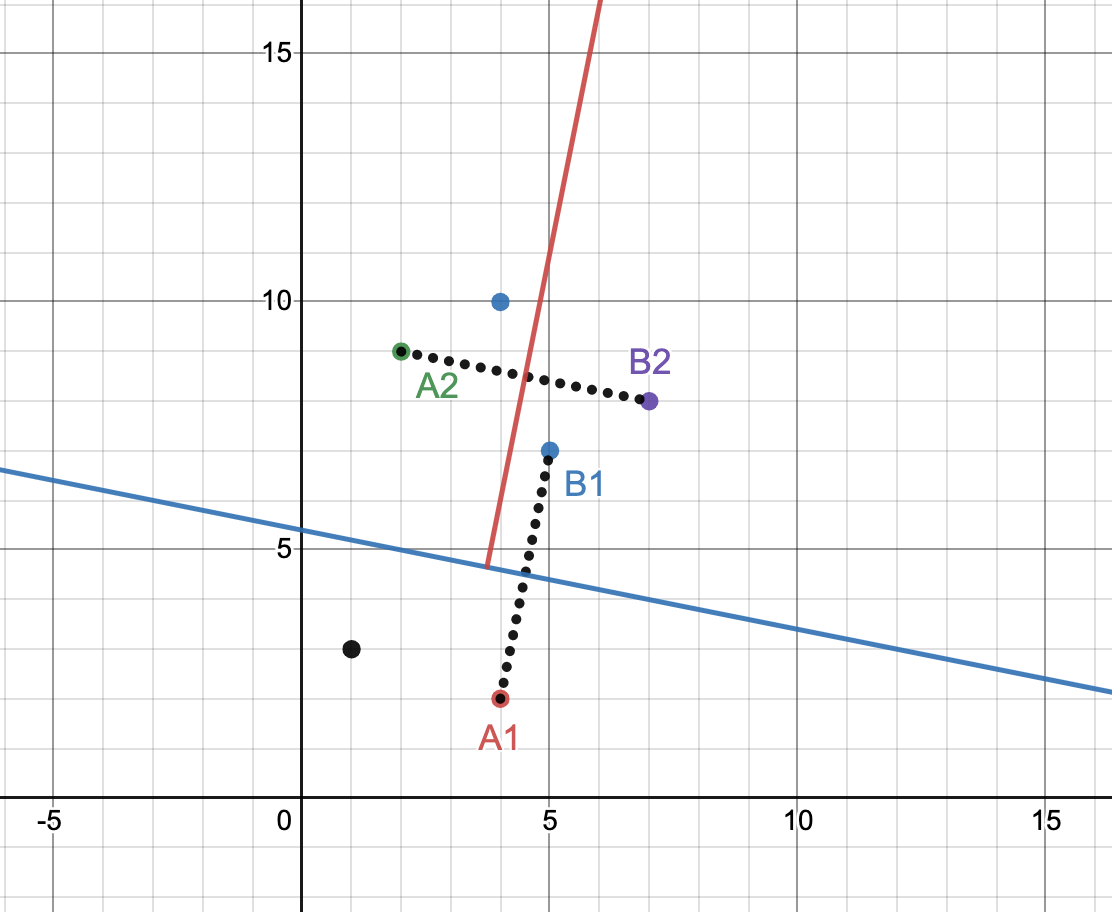
图(1): 用随机超平面分割空间
我们随机选择向量 A1=(4,2), B1=(5,7).它们的中点是 (4.5,4.5),我们通过中点垂直于线 (A1, B1) 构建一条线.那条线是 x + 5y=27(以蓝色绘制),它给我们一组 2 个向量,一组 4 个.假设最大节点大小配置为 2.我们不进一步拆分第一组,而是选择一个新的 (A2, B2) 从后者构建红色超平面等等.对大型数据集的重复拆分将超空间拆分为几个不同的区域,如下所示

图(2): 许多超平面后的分段空间
这里的每个区域代表一个叶节点,这里的直觉是足够接近的点很可能最终出现在同一个叶节点中.因此,给定一个查询点,我们可以以对数时间向下遍历树以定位它所属的叶子并对叶子中的所有(少量)点运行线性扫描.这显然不是万无一失的 —— 实际上足够近的点完全有可能被一个超平面分开,最终彼此相距很远.但是这个问题可以通过构建多棵独立树而不是一棵树来解决 —— 这样,如果两点足够近,它们更有可能位于至少某些树中的同一叶节点中.在查询时,我们向下遍历所有树以定位相关的叶节点,对所有叶节点的所有候选节点进行并集,并对所有节点进行线性扫描
#[derive(Eq, PartialEq, Hash)]
pub struct HashKey<const N: usize>([u32; N]);
#[derive(Copy, Clone)]
pub struct Vector<const N: usize>(pub [f32; N]);
impl<const N: usize> Vector<N> {
pub fn subtract_from(&self, vector: &Vector<N>) -> Vector<N> {
let mapped = self.0.iter().zip(vector.0).map(|(a, b)| b - a);
let coords: [f32; N] = mapped.collect::<Vec<_>>().try_into().unwrap();
return Vector(coords);
}
pub fn avg(&self, vector: &Vector<N>) -> Vector<N> {
let mapped = self.0.iter().zip(vector.0).map(|(a, b)| (a + b) / 2.0);
let coords: [f32; N] = mapped.collect::<Vec<_>>().try_into().unwrap();
return Vector(coords);
}
pub fn dot_product(&self, vector: &Vector<N>) -> f32 {
let zipped_iter = self.0.iter().zip(vector.0);
return zipped_iter.map(|(a, b)| a * b).sum::<f32>();
}
pub fn to_hashkey(&self) -> HashKey<N> {
// f32 in Rust doesn't implement hash. We use bytes to dedup. While it
// can't differentiate ~16M ways NaN is written, it's safe for us
let bit_iter = self.0.iter().map(|a| a.to_bits());
let data: [u32; N] = bit_iter.collect::<Vec<_>>().try_into().unwrap();
return HashKey::<N>(data);
}
pub fn sq_euc_dis(&self, vector: &Vector<N>) -> f32 {
let zipped_iter = self.0.iter().zip(vector.0);
return zipped_iter.map(|(a, b)| (a - b).powi(2)).sum();
}
}
构建完这些核心实用程序后,我们还可以定义超平面的外观:
struct HyperPlane<const N: usize> {
coefficients: Vector<N>,
constant: f32,
}
impl<const N: usize> HyperPlane<N> {
pub fn point_is_above(&self, point: &Vector<N>) -> bool {
self.coefficients.dot_product(point) + self.constant >= 0.0
}
}
如何表示树 🌲 中的点
我们可以直接将 D 维向量存储在叶节点中.但是,对于大 D,这会显着碎片化内存(主要性能影响),并且当多棵树引用相同的向量时,还会在森林中创建重复内存.相反,我们将向量存储在全局连续位置,并在叶节点处保存 usize 索引(在 64 位系统上为 8 字节而不是 4D,其中 f32 占用 4 字节).以下是用于表示树的内部节点和叶节点的数据类型
enum Node<const N: usize> {
Inner(Box<InnerNode<N>>),
Leaf(Box<LeafNode<N>>),
}
struct LeafNode<const N: usize>(Vec<usize>);
struct InnerNode<const N: usize> {
hyperplane: HyperPlane<N>,
left_node: Node<N>,
right_node: Node<N>,
}
pub struct ANNIndex<const N: usize> {
trees: Vec<Node<N>>,
ids: Vec<i32>,
values: Vec<Vector<N>>,
}
找到正确的超平面
对向量 A 和 B 采样两个唯一索引,计算 n = A - B,并找到 A 和 B 的中点(point_on_plane).超平面使用系数向量 n和常量(n 和 point_on_plane 的点积)结构有效地存储为 n(x-x0) = nx - nx0.我们可以在任何向量和 n 之间执行点积,然后减去常数以将向量放在超平面“上方”或“下方”.由于树中的内部节点包含超平面定义,叶节点包含向量 ID,因此我们可以使用 ADT 对树进行类型检查:
impl<const N: usize> ANNIndex<N> {
fn build_hyperplane(
indexes: &Vec<usize>,
all_vecs: &Vec<Vector<N>>,
) -> (HyperPlane<N>, Vec<usize>, Vec<usize>) {
let sample: Vec<_> = indexes
.choose_multiple(&mut rand::thread_rng(), 2)
.collect();
// cartesian eq for hyperplane n * (x - x_0) = 0
// n (normal vector) is the coefs x_1 to x_n
let (a, b) = (*sample[0], *sample[1]);
let coefficients = all_vecs[a].subtract_from(&all_vecs[b]);
let point_on_plane = all_vecs[a].avg(&all_vecs[b]);
let constant = -coefficients.dot_product(&point_on_plane);
let hyperplane = HyperPlane::<N> {
coefficients,
constant,
};
let (mut above, mut below) = (vec![], vec![]);
for &id in indexes.iter() {
if hyperplane.point_is_above(&all_vecs[id]) {
above.push(id)
} else {
below.push(id)
};
}
return (hyperplane, above, below);
}
}
我们可以定义我们的递归过程以基于索引时间“最大节点大小”构建树:
impl<const N: usize> ANNIndex<N> {
fn build_a_tree(
max_size: i32,
indexes: &Vec<usize>,
all_vecs: &Vec<Vector<N>>,
) -> Node<N> {
if indexes.len() <= (max_size as usize) {
return Node::Leaf(Box::new(LeafNode::<N>(indexes.clone())));
}
let (plane, above, below) = Self::build_hyperplane(indexes, all_vecs);
let node_above = Self::build_a_tree(max_size, &above, all_vecs);
let node_below = Self::build_a_tree(max_size, &below, all_vecs);
return Node::Inner(Box::new(InnerNode::<N> {
hyperplane: plane,
left_node: node_below,
right_node: node_above,
}));
}
}
⚠️ 请注意,在两点之间构建超平面需要这两点是唯一的 - 即我们必须在索引之前对向量集进行去重,因为该算法不允许重复
因此整个索引(树的森林)可以这样构建:
impl<const N: usize> ANNIndex<N> {
fn deduplicate(
vectors: &Vec<Vector<N>>,
ids: &Vec<i32>,
dedup_vectors: &mut Vec<Vector<N>>,
ids_of_dedup_vectors: &mut Vec<i32>,
) {
let mut hashes_seen = HashSet::new();
for i in 1..vectors.len() {
let hash_key = vectors[i].to_hashkey();
if !hashes_seen.contains(&hash_key) {
hashes_seen.insert(hash_key);
dedup_vectors.push(vectors[i]);
ids_of_dedup_vectors.push(ids[i]);
}
}
}
pub fn build_index(
num_trees: i32,
max_size: i32,
vecs: &Vec<Vector<N>>,
vec_ids: &Vec<i32>,
) -> ANNIndex<N> {
let (mut unique_vecs, mut ids) = (vec![], vec![]);
Self::deduplicate(vecs, vec_ids, &mut unique_vecs, &mut ids);
// Trees hold an index into the [unique_vecs] list which is not
// necessarily its id, if duplicates existed
let all_indexes: Vec<usize> = (0..unique_vecs.len()).collect();
let trees: Vec<_> = (0..num_trees)
.map(|_| Self::build_a_tree(max_size, &all_indexes, &unique_vecs))
.collect();
return ANNIndex::<N> {
trees,
ids,
values: unique_vecs,
};
}
}
查询时间
建立索引后,我们如何使用它在单个树上搜索输入向量的 K 个近似最近邻?在非叶节点处,我们存储超平面,因此我们可以从树的根开始并询问:“这个向量是在这个超平面之上还是之下?”.这可以用点积在 O(D) 中计算.根据响应,我们可以递归搜索左子树或右子树,直到找到叶节点.请记住,叶节点最多存储“最大节点大小”向量,这些向量位于输入向量的近似邻域内(因为它们落在所有超平面下的超空间的同一分区中,请参见图 1(b)).如果这个叶节点的向量索引数超过 K,我们现在可以按照到输入向量的 L2 距离对所有这些向量进行排序,并返回最接近的 K!
假设我们的索引导致一棵平衡树,对于维度 D、向量数 N 和最大节点大小 M << N,搜索需要 O(Dlog(N) + DM + Mlog(M)) - 这构成了平均最差- case log(N) 超平面比较找到一个叶子节点(也就是树的高度),其中每次比较花费 O(D) 点积,在 O(DM) 中计算一个叶子节点中所有候选向量的 L2 度量最后对它们进行排序以返回 O(Mlog(M)) 中的前 K 个
但是,如果我们找到的叶节点少于 K 个向量,会发生什么情况?如果最大节点大小太小或存在相对不均匀的超平面分裂,则可能会在子树中留下非常少的向量.为了解决这个问题,我们可以在树搜索中添加一些简单的回溯功能.例如,如果返回的候选项数量不足,我们可以在内部节点进行额外的递归调用以访问另一个分支.这就是它的样子:
impl<const N: usize> ANNIndex<N> {
fn tree_result(
query: Vector<N>,
n: i32,
tree: &Node<N>,
candidates: &mut HashSet<usize>,
) -> i32 {
// take everything in node, if still needed, take from alternate subtree
match tree {
Node::Leaf(box_leaf) => {
let leaf_values = &(box_leaf.0);
let num_candidates_found = min(n as usize, leaf_values.len());
for i in 0..num_candidates_found {
candidates.insert(leaf_values[i]);
}
return num_candidates_found as i32;
}
Node::Inner(inner) => {
let above = (*inner).hyperplane.point_is_above(&query);
let (main, backup) = match above {
true => (&(inner.right_node), &(inner.left_node)),
false => (&(inner.left_node), &(inner.right_node)),
};
match Self::tree_result(query, n, main, candidates) {
k if k < n => {
k + Self::tree_result(query, n - k, backup, candidates)
}
k => k,
}
}
}
}
}
请注意,我们还可以通过存储子树中的向量总数和直接指向每个内部节点的所有叶节点的指针列表来进一步优化递归调用,但为简单起见,此处不这样做
将此搜索扩展到树木森林是微不足道的 - 只需从所有树木中独立收集前 K 个候选者,按距离对它们进行排序,然后返回总体前 K 个匹配项.请注意,更多的树将具有线性高的内存占用和线性缩放的搜索时间,但可以导致更好的“更近”邻居,因为我们收集了不同树的候选者
impl<const N: usize> ANNIndex<N> {
pub fn search_approximate(
&self,
query: Vector<N>,
top_k: i32,
) -> Vec<(i32, f32)> {
let mut candidates = HashSet::new();
for tree in self.trees.iter() {
Self::tree_result(query, top_k, tree, &mut candidates);
}
candidates
.into_iter()
.map(|idx| (idx, self.values[idx].sq_euc_dis(&query)))
.sorted_by(|a, b| a.1.partial_cmp(&b.1).unwrap())
.take(top_k as usize)
.map(|(idx, dis)| (self.ids[idx], dis))
.collect()
}
}
这在 200 行 Rust 中为我们提供了一个简单的向量搜索索引!
补充
此示例跳过了几个对生产向量搜索至关重要的注意事项:
当搜索涉及多棵树时并行化.我们可以并行化而不是按顺序收集候选者,因为每棵树都访问不同的内存——每棵树都可以在单独的线程上运行,候选者通过通道中的消息不断地发送到主进程.线程可以在索引时间本身产生,并通过虚拟搜索(树的部分位于缓存中)进行预热,以减少搜索开销.搜索将不再按树的数量线性扩展.
大树可能不适合 RAM,需要有效的方法从磁盘读取 - 某些子图可能需要在磁盘上,并且算法设计为允许搜索同时最小化文件 I/O.
更进一步,如果树不适合实例的磁盘,我们需要跨实例分布子树,并且如果数据在本地不可用,递归搜索调用会触发一些
RPC 请求.该树涉及许多内存重定向(基于指针的树对 L1 缓存不友好).平衡树可以用数组很好地编写,但我们的树仅与随机超平面接近平衡——我们可以为树使用新的数据结构吗?
当新数据被动态索引时(可能需要对大树重新分片),上述问题的解决方案也应该适用.如果某个索引序列导致树高度不平衡,是否应该重新创建树?